I've made a previous post about Specific Impulse, but I've wanted to improve it for a while, since it's not very clear. This post is using a new system called MathJax to display equations, which should make them easier to read.
Specific impulse is essentially a measure of how efficiently a rocket engine converts the chemical potential energy of its fuel into the kinetic energy driving the rocket forward. It is defined as the thrust of a rocket engine $T$ divided by the weight flow rate $\dot{W}$: $$I_{sp}=\frac{T}{\dot{W}}$$ First, we need to distinguish between weight and mass. Mass is how much matter an object consists of, while weight is the force exerted on an object by the local gravitational field. The local gravity on Earth exerts 9.81 m/s^2 of acceleration on everything, so if force = mass times acceleration, the force, or weight, exerted by an object with 1 kg of mass is 1 kg * 9.81 m/s^2. Since one Newton is the amount of force needed to accelerate one kg at 1 m/s^2, the object has a weight of 9.81 N. Weight is normally measured in kilograms (or pounds, but they're the same dimensionally), which seems odd, since we know weight can change independently of mass on different planets with different gravities. This is because the unit commonly referred to by a kilogram is actually kilogram-force, or a kilopond, which is exactly the force of one kilogram of mass in standard Earth gravity, or about 9.81 N. Therefore, in common use, both the definition and unit of mass and weight are the same.
Specific impulse $I_{sp}$ is defined as the thrust $T$ produced by a rocket engine, divided by the weight flow rate of propellant $\dot{W}$, or: $${I_{sp}}=\frac{T}{\dot{W}}$$ It seems like it should be thrust per unit weight of propellant consumed, but thrust is instantaneous, so it wouldn't make sense without converting to some weird unit like newton-seconds.
Since $\dot{W}$ is weight, and weight is mass multiplied by standard gravity, the weight flow rate is the mass flow rate $\dot{m}$ multiplied by gravity: $$\dot{W}=g\dot{m}$$ The mass flow rate is the first derivative of the propellant mass $m_p$ with respect to time: $$\dot{m}=\frac{dm_p}{dt}$$ Therefore: $$\dot{W}=g\frac{dm_p}{dt}$$
Thrust is simply the exhaust velocity of the propellant from the engine $v_e$ multiplied by the mass flow rate $\dot{m}$ which is exactly the same as the mass flow rate already defined: $$T=v_e\frac{dm_p}{dt}$$
If we substitute these back into the original $I_{sp}$ formula, we get: $$I_{sp}=\frac{v_e\frac{dm_p}{dt}}{g\frac{dm_p}{dt}}$$ Since the mass flow rate is on both the top and bottom of the equation, we can get rid of them, and get: $$I_{sp}=\frac{v_e}{g}$$ The important thing to remember here is that $g$ is a constant in this equation. It is quite literally the acceleration due to gravity at the earth's surface, regardless of where the rocket engine is, or what kind of gravity it is in. In fact, any constant with the unit of $m/s^2$ would work. Not only that, but when calculating $\Delta{V}$ using a specific impulse term, as is frequently seen, the specific impulse term is multiplied by $g$, turning the term back into $v_e$. Another weird effect of this is that specific impulse has a unit of seconds.
This weird definition was originally used, as far as I can tell, because the unit of seconds is the same whether you're using metric or imperial units to calculate it, which is less confusing than m/s and ft/s. Using metric units, exhaust velocity and specific impulse can be calculated approximately by multiplying or dividing by ten. In short, specific impulse is a way of making exhaust velocity, which is the real measure of rocket engine efficiency, into a number which is the same whatever units you use to calculate it.
Interestingly, $v_e$ is effective exhaust velocity, which takes into account any propellant not exhausted at the full velocity of the engine, such as with turbine exhaust or film cooling. Effective exhaust velocity can be calculated on an existing engine with the specific impulse formula by using: $$v_e=\frac{T}{\dot{m}}$$ Except $T$ and $\dot{m}$ are based on measurements of a engine rather than calculated.
Showing posts with label efficiency. Show all posts
Showing posts with label efficiency. Show all posts
Monday, May 21, 2018
Wednesday, February 10, 2016
Gravity turn
When you watch a rocket launch, you see that it gently tips over as it climbs. This is because to stay in orbit, a vehicle must travel sideways, very fast. However, it must also climb above the atmosphere. Obviously, going straight up until you reach space, then turning 90 degrees and going into orbit is inefficient, and going sideways immediately after launch is also inefficient. So what do rockets do?
First, there are three terms we must familiarize ourselves with: gravity losses, drag losses, and steering losses.
These term refer to things which require delta-v aside from expending delta-v just to increase your total speed in a vacuum. So your total speed after expending all propellant would be total potential delta-v (if your rocket was going in one direction in a vacuum with no gravitational losses) minus gravity losses, drag losses, and steering losses.
Gravity losses are the delta-v expended that is just fighting against gravity, instead of speeding up the vehicle. To imagine this, think of a rocket with a thrust to weight ratio of exactly 1, that is hovering just above the launchpad. This rocket, in free space, could accelerate to 1,000 m/s, but, because gravity losses take up all of the potential delta-v, it's end speed is zero.
Drag losses: if your rocket expends 1,000 m/s of delta-v in a gravity-less vacuum, you end up travelling at 1,000 m/s. However, if you put an atmosphere in that vacuum which your rocket must travel through, then drag will slow the rocket down, even as it continues to accelerate. The difference between the total potential delta-v and your end speed is the drag losses.
Steering losses: you have a total potential delta-v of 1,000 m/s, and you expend 500 m/s going in one direction in a gravity-less vacuum, then you turn around 180 degrees and expend the remaining 500 m/s. Your end speed is zero, because your steering losses are 1,000 m/s.
Back to gravity turns. A gravity turn is the optimized curve from vertical to horizontal of a rocket traveling to orbit. Because a rocket "balances" on its engines, gravity slowly pulls the front of the rocket down, which works efficiently, because less delta-v is needed for steering the rocket, and because the angle of attack (angle of the rocket to the air it's passing through) in almost zero throughout the entire ascent. An ideal one will have a minimum of drag, gravity, and steering losses. Turning too sharply to early will result in high steering losses, and turning too late will result in high steering losses.
Ideally there should only need to be one steering event, at the very start of the gravity turn, pitching over 5-10 degrees while the rocket is still fairly low in the atmosphere. Then gravity should take over.
Labels:
atmosphere,
delta-v,
delta-v losses,
drag,
Earth,
efficiency,
gravity,
gravity turn,
launch,
m/s,
rocket,
steering,
vacuum
Thursday, October 1, 2015
Rocket engines
Today we're going to look at rocket engines. Rocket engines are some of the most complex things in existence. They operate at incredible extremes, and yet they are very complex. Here's a test fire of a Merlin 1D rocket engine:
A rocket engine is very similar in concepts to a jet engine, with one difference: A jet engine collects oxidizer from the ambient air, but a rocket is completely self contained and self propelled. It carries all its fuel with it, so rocket engines have to combine fuel and oxidizer, ignite it, and propel it out at supersonic speeds.
The concepts behind rocket engines are simple, if not the implementations. A rocket is a lot like an inflated party balloon. The air in an inflated balloon is the fuel. It stretches the rubber skin, adding potential energy, and then is propelled by that energy out of the hole in the balloon, and the mass expelled from the balloon drives it across the room. Technically, a balloon is a pressure fed, monopropellant rocket.
There are a lot of kinds of rocket engines, but we'll start by looking at the most common kind: The liquid bipropellant rocket engine.
The fuel and oxidizer from the rocket's tanks are sucked from the tanks by high speed turbopumps. To give you an example, the J-2X hydrogen turbopump produces an incredible 16,000 horsepower. Where they go from there depends on the rocket. Somehow, the fuel is expanded to propel the turbo part of the turbopumps, either by being burnt with the oxidizer in a small combustion chamber and then sent to the turbopumps, if it's a gas generator cycle engine, sent around the engine to be heated up if it's an expander cycle engine, or fed through a pre-burner, which is very similar to a gas generator, except that the exhaust is fed back into the main combustion chamber to be burnt again after it's been used to power the turbopumps.
This is only a very basic overview of the different ways of dealing with turbopumps, for a more in-depth look at it see this blog's post. Actually, read all of the posts. No really, this is an great blog. All of the posts are interesting and relevant, especially to this post. Also, look at this video, from Copenhagen Suborbitals:
The fuel (and sometimes oxidizer) is then pumped through tubes in the walls of the main combustion chamber (MCC) and the nozzle walls. After that, it gets really interesting. The fuel and oxidizer is then combined and burnt in the MCC. The cold fuel flowing through the walls prevents the MCC from melting.
When fuel and oxidizer have been burnt in the MCC, the combustion products are forced out of the MCC, into the throat of the nozzle. This part is like that thing that you can put on the end of a garden hose to increase the fluid speed and decrease fluid pressure. This is known as the Venturi effect. However, the Venturi effect only works with subsonic fluids, if the fluid is supersonic, the flow "chokes" because the pressure waves that cause the Venturi effect no longer propagate upstream, instead, a diverging tube will increase speed and decrease pressure at supersonic speeds. This is the principle that makes the de Laval nozzle work, which is used in most liquid rocket engines. It is named after a Swedish inventor, Gustaf de Laval.
Here's a picture of a cross section of a de Laval nozzle:

"Laval-nozzle-(longitudinal-section-of-RD-107-jet-engine)" by Albina-belenkaya - Own work. Licensed under CC BY-SA 4.0 via Commons.
You can see how, after the exhaust has been accelerated to supersonic speeds by the nozzle converging from the MCC at the top of the picture, the nozzle diverges to further increase the speed.
Again, take a look at this blog for a more in-depth article about this.
Rocket engines are built differently for different environments. At sea level, engine nozzles are shaped differently than vacuum engine nozzles, because that the ambient pressure is higher, so nozzles need to be shaped differently to get the most thrust in the environment it's designed for.
Some rockets have hydraulic actuators which swivel the engine to provide steering while the engine's providing thrust, by changing the angle of thrust through the rocket. The hydraulic actuators are powered by the rocket engine itself. Here's a video of a J-2X engine being gimbal tested:
So how do you provide fuel to an engine that's rotating relative to the tanks? By using pipes with bellows. It seems pretty simple, except you have to remember, these pipes have less than -183 degrees Celsius liquid oxygen being forced through them, and, in some engines, even colder liquid hydrogen being pumped through them.
I'll finish this post with a video of a Copenhagen Suborbitals rocket being explained (This is a pressure fed, liquid chemical bi-propellent rocket engine):
Curious about what happened in the test? Look here.
A rocket engine is very similar in concepts to a jet engine, with one difference: A jet engine collects oxidizer from the ambient air, but a rocket is completely self contained and self propelled. It carries all its fuel with it, so rocket engines have to combine fuel and oxidizer, ignite it, and propel it out at supersonic speeds.
The concepts behind rocket engines are simple, if not the implementations. A rocket is a lot like an inflated party balloon. The air in an inflated balloon is the fuel. It stretches the rubber skin, adding potential energy, and then is propelled by that energy out of the hole in the balloon, and the mass expelled from the balloon drives it across the room. Technically, a balloon is a pressure fed, monopropellant rocket.
There are a lot of kinds of rocket engines, but we'll start by looking at the most common kind: The liquid bipropellant rocket engine.
The fuel and oxidizer from the rocket's tanks are sucked from the tanks by high speed turbopumps. To give you an example, the J-2X hydrogen turbopump produces an incredible 16,000 horsepower. Where they go from there depends on the rocket. Somehow, the fuel is expanded to propel the turbo part of the turbopumps, either by being burnt with the oxidizer in a small combustion chamber and then sent to the turbopumps, if it's a gas generator cycle engine, sent around the engine to be heated up if it's an expander cycle engine, or fed through a pre-burner, which is very similar to a gas generator, except that the exhaust is fed back into the main combustion chamber to be burnt again after it's been used to power the turbopumps.
This is only a very basic overview of the different ways of dealing with turbopumps, for a more in-depth look at it see this blog's post. Actually, read all of the posts. No really, this is an great blog. All of the posts are interesting and relevant, especially to this post. Also, look at this video, from Copenhagen Suborbitals:
The fuel (and sometimes oxidizer) is then pumped through tubes in the walls of the main combustion chamber (MCC) and the nozzle walls. After that, it gets really interesting. The fuel and oxidizer is then combined and burnt in the MCC. The cold fuel flowing through the walls prevents the MCC from melting.
When fuel and oxidizer have been burnt in the MCC, the combustion products are forced out of the MCC, into the throat of the nozzle. This part is like that thing that you can put on the end of a garden hose to increase the fluid speed and decrease fluid pressure. This is known as the Venturi effect. However, the Venturi effect only works with subsonic fluids, if the fluid is supersonic, the flow "chokes" because the pressure waves that cause the Venturi effect no longer propagate upstream, instead, a diverging tube will increase speed and decrease pressure at supersonic speeds. This is the principle that makes the de Laval nozzle work, which is used in most liquid rocket engines. It is named after a Swedish inventor, Gustaf de Laval.
Here's a picture of a cross section of a de Laval nozzle:

"Laval-nozzle-(longitudinal-section-of-RD-107-jet-engine)" by Albina-belenkaya - Own work. Licensed under CC BY-SA 4.0 via Commons.
You can see how, after the exhaust has been accelerated to supersonic speeds by the nozzle converging from the MCC at the top of the picture, the nozzle diverges to further increase the speed.
Again, take a look at this blog for a more in-depth article about this.
Rocket engines are built differently for different environments. At sea level, engine nozzles are shaped differently than vacuum engine nozzles, because that the ambient pressure is higher, so nozzles need to be shaped differently to get the most thrust in the environment it's designed for.
Some rockets have hydraulic actuators which swivel the engine to provide steering while the engine's providing thrust, by changing the angle of thrust through the rocket. The hydraulic actuators are powered by the rocket engine itself. Here's a video of a J-2X engine being gimbal tested:
So how do you provide fuel to an engine that's rotating relative to the tanks? By using pipes with bellows. It seems pretty simple, except you have to remember, these pipes have less than -183 degrees Celsius liquid oxygen being forced through them, and, in some engines, even colder liquid hydrogen being pumped through them.
I'll finish this post with a video of a Copenhagen Suborbitals rocket being explained (This is a pressure fed, liquid chemical bi-propellent rocket engine):
Curious about what happened in the test? Look here.
Labels:
ASL,
copsub,
efficiency,
engine,
fuel,
j-2x,
laval,
mcc,
merlin,
oxidizer,
propellent,
rocket
Wednesday, September 2, 2015
Specific impulse
Our topic for today is another rocketry concept: Specific impulse (usually abbreviated Isp). Basically, it's how efficient your rocket engine is. It's defined by how far each unit of fuel moves your rocket.
Here's the formula:
 Where:
Where:
If your Isp is higher, then you can get more Delta-V with the same rocket. In the rocket equation,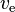 is used instead of Isp, but the concepts are the same.
is used instead of Isp, but the concepts are the same.
Here's the formula:
 Where:
Where: 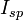 is the specific impulse in meters per second
is the specific impulse in meters per second the thrust in newtons
the thrust in newtons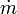 the fuel consumption in kg/s
the fuel consumption in kg/s
If your Isp is higher, then you can get more Delta-V with the same rocket. In the rocket equation,
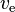 is used instead of Isp, but the concepts are the same.
is used instead of Isp, but the concepts are the same.
Subscribe to:
Posts (Atom)